Cos’è il paradosso di Simpson e cosa c’entra con i vaccini

Quando si analizzano i dati sull’efficacia dei vaccini si rischia di incorrere nel paradosso di Simpson e di avere un’immagine distorta di come i vaccini ci stanno proteggendo dalla Covid-19.

Cos’è il paradosso di Simpson

Il paradosso di Simpson è un concetto relativamente semplice: consiste nel vedere una tendenza quando i dati sono divisi per gruppi, tendenza che però sparisce o diminuisce quando gli stessi dati sono invece presentati tutti insieme. 

Uno dei casi più famosi dell’applicazione di questo paradosso fu quando l’Università di Berkeley fu accusata nel 1973 di avere un pregiudizio di genere nell’ammissione ai suoi corsi, avendo ammesso il 44% dei candidati maschi e solo il 35% di candidate femmine. L’università chiese allo statistico Pete Bickel di esaminare i dati in vista della causa per capire se ci fosse davvero un pregiudizio: Bickel scoprì che in realtà in quattro dei sei dipartimenti c’era un pregiudizio significativo addirittura a favore delle donne, mentre in due dipartimenti non si era riscontrato nessun pregiudizio di genere. Si scoprì così che le donne tendevano a fare domanda nei dipartimenti che ammettevano meno persone nel complesso, e che questa variabile influenzava i valori totali andando a invertire la tendenza totale dei dati. 

L’immagine di seguito mostra graficamente in che cosa consiste questo paradosso: se prendiamo tutti i dati insieme (immagine a sinistra) vediamo che la variabile y cresce al crescere della variabile x, mentre se dividiamo in due i gruppi (immagine a destra) osserviamo che invece la variabile y diminuisce al crescere di x.

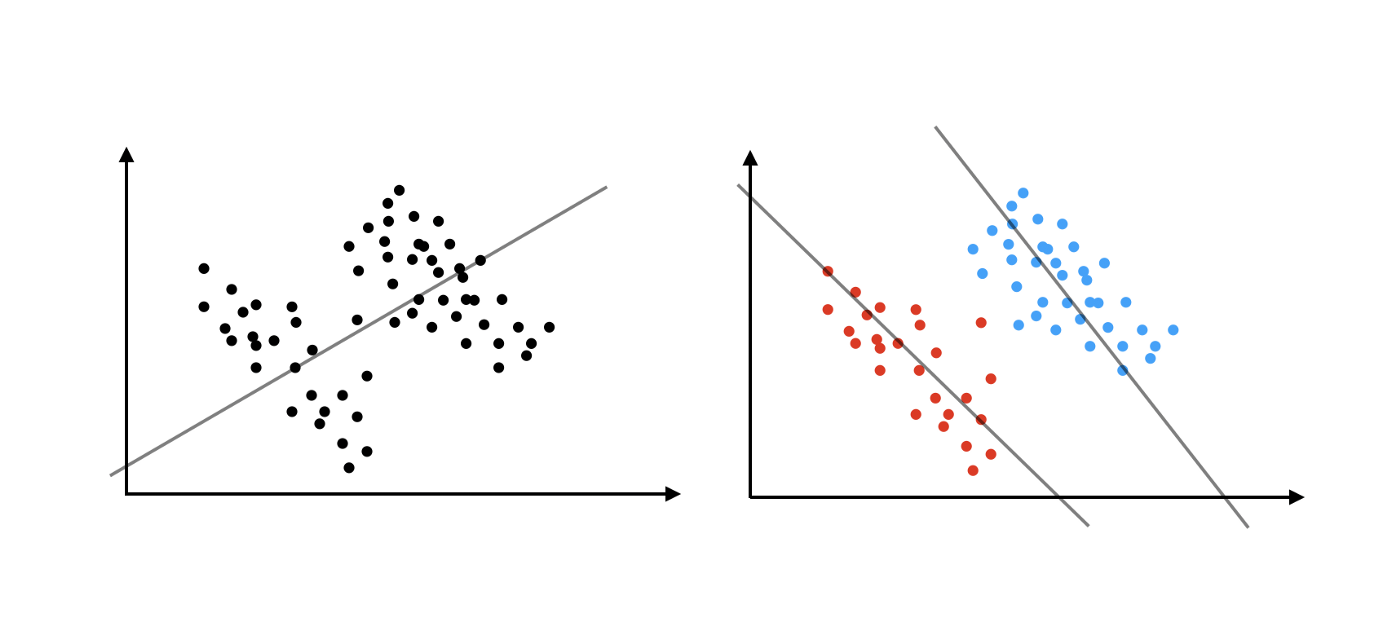
Fonte: Towards data science.

Ma cosa c’entra con i vaccini?

Come avevamo spiegato la settimana scorsa, per capire quanto i vaccini per la Covid-19 funzionino bene bisogna guardare alle diverse incidenze tra completamente vaccinati, parzialmente vaccinati e non vaccinati, guardando come questi dati tendono a ridurre i dati di contagi, ricoveri e decessi.

Facciamo un esempio concreto guardando al dato sui decessi: tra chi ha ricevuto una diagnosi di positività tra il 30 luglio e il 29 agosto ed è poi morto, si sono registrati 1,6 decessi ogni 100.000 persone completamente vaccinate e 5,6 ogni 100.000 persone non vaccinate. Rispetto ai non vaccinati, tra i completamente vaccinati si è avuta quindi una riduzione del 72% dell’incidenza. Guardiamo ora alle riduzioni per fascia di età: 78% per i 12-39enni (dato statisticamente non significativo perché si tratta di pochissime persone), 94% per i 40-59enni, 94% per i 60-79enni e 92% per gli over 89. 

I dati italiani sui decessi mostrano quindi che quando guardiamo alla riduzione complessiva dell’incidenza siamo al 72%, ma se guardiamo per gruppi anagrafici si va dal 78% fino al 94% tra le fasce di età più vulnerabili al virus. Aggregare i dati porta quindi a una riduzione della tendenza. 

Questo si verifica perché il rischio di morire e il tasso di vaccinazione sono più alti tra gli anziani che tra i giovani. Quando non si stratifica per età, quindi, a causa del paradosso di Simpson si ha un risultato paradossale che porta ad avere un’efficacia complessiva che è più bassa dell’efficacia di ogni gruppo d’età.

Il rischio di morire quando si contrae la Covid-19 per un 30enne è di 8 volte inferiore rispetto a una persona di 50 anni, 19 volte inferiore rispetto a una di 60 anni, 68 volte inferiore di una di 7o anni e ben 320 volte inferiore rispetto a un ottantenne. Il tasso di vaccinazione degli over 80 è del 96%, per i 70-79enni del 92%, per i 60-69enni del 90%, per i 50-59enni dell’85% e per i 30-39enni del 78%. 

Conclusione

L’efficacia dei vaccini è un chiaro esempio di quanto si debba fare attenzione ad analizzare i dati di fenomeni che presentano distribuzioni di probabilità che cambiano molto a seconda del gruppo che si sta guardando. Disaggregando per fascia anagrafica si vede che i vaccini funzionano estremamente bene contro il rischio di morire, ma aggregando tutto insieme l’efficacia complessiva sembrerebbe invece scendere a causa del paradosso di Simpson, prestando il fianco a strumentalizzazioni che davvero nulla hanno a che fare con i dati e con la scienza.