Qual è la probabilità di essere davvero positivi con un test positivo?

In queste settimane in Italia c’è stata un’esplosione del numero di test rapidi eseguiti quotidianamente per capire se si è positivi al Sars-Cov-2 a causa della progressiva diffusione della variante Omicron. Questi test vengono spesso accusati di non essere abbastanza affidabili. Ma è davvero così? Come si interpreta effettivamente il risultato di un test? 

La probabilità di essere positivo se testato positivo

Quando valutiamo un test dobbiamo guardare alla sensibilità e alla specificità. La prima è la proporzione di positivi identificati correttamente come positivi al coronavirus (un’alta sensibilità corrisponde a pochi falsi negativi), mentre la seconda è la proporzione di negativi che sono correttamente identificati come negativi al coronavirus (un’alta specificità corrisponde a pochi falsi positivi). 

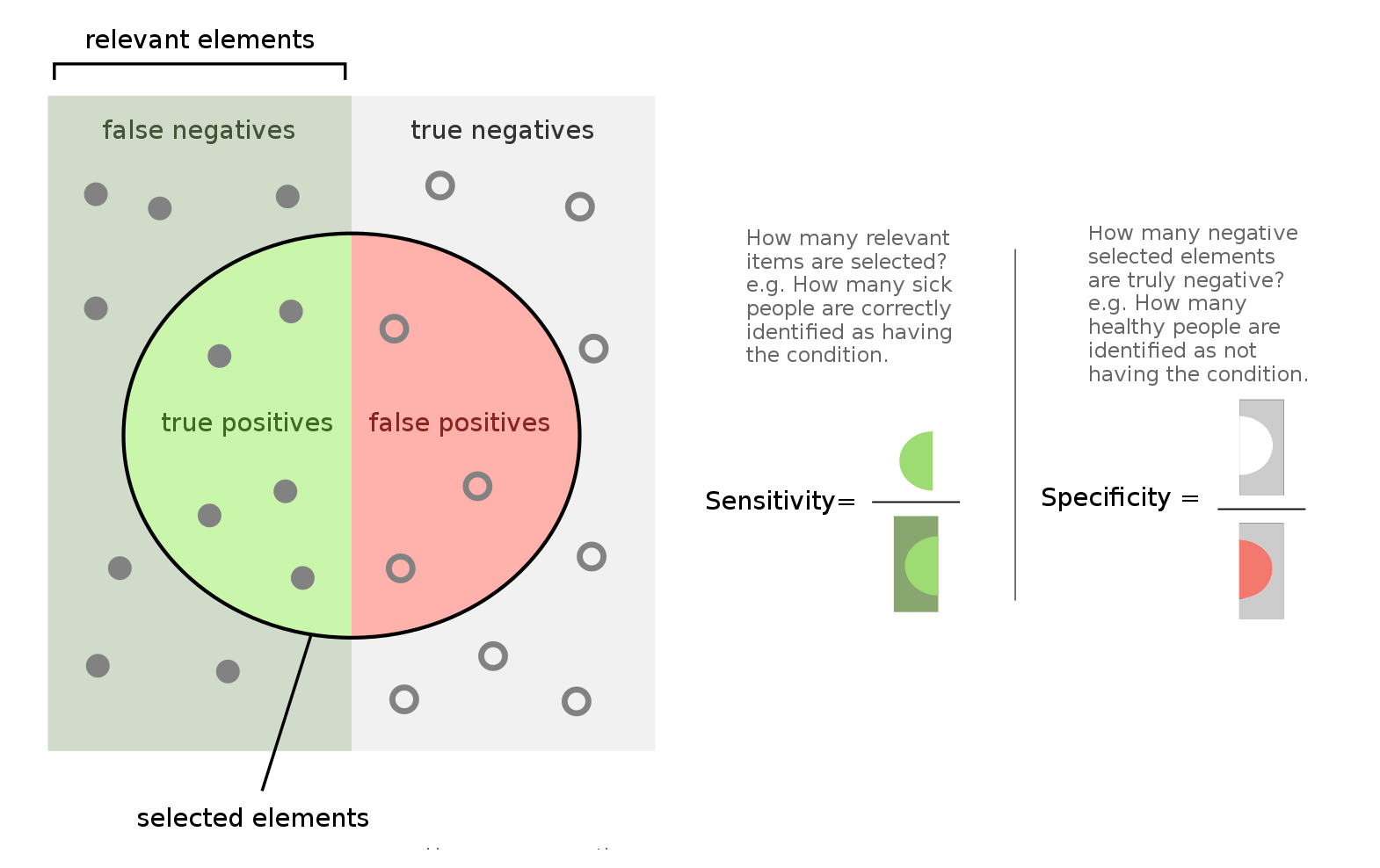
Fonte immagine: Wikipedia

Per identificare correttamente i positivi al coronavirus, quindi, è necessario che il test abbia un’alta sensibilità. Ma questo non è sufficiente, perché manca un’informazione: qual è la probabilità a priori di essere positivi?

Per rispondere serve il teorema di Bayes, secondo cui la probabilità che una persona abbia il coronavirus dopo un test risultato positivo (P(C|T)) è dal rapporto tra, a numeratore, la probabilità di avere un test positivo se si ha il coronavirus (P(T|C), la sensibilità) moltiplicata per la probabilità di avere il coronavirus data la sua diffusione (P(C)) e, a denominatore, la probabilità di risultati positivi indipendentemente dal fatto che lo si sia o meno (P(T)).

In formula, il teorema di Bayes è: P(C|T) = P(T|C) *P(C) / P(T).

Facciamo un esempio concreto: supponiamo di avere un test estremamente accurato che ha una sensibilità del 99% e una specificità del 99%. Il test rivela però una malattia poco diffusa nella popolazione, che ipotizziamo avere una persona ogni 10.000. Quest’ultima è la probabilità “a priori”.

Ora prendiamo casualmente un milione di persone. Sappiamo, basandoci sulla probabilità a priori, che 100 persone hanno la malattia e 999.900 non la hanno. Delle persone che hanno la malattia il nostro test ne identificherà correttamente 99 (100*99/100) e di quelle che non la hanno 989.901 (999.900*99/100). Il nostro test quindi avrà detto a 9.999 persone (999.900 – 989.901) che sono positive anche se non lo sono realmente. A questo punto quindi la probabilità di avere realmente la malattia è 99 su 10.098 (99 + 9.999), ossia lo 0,98%. 

Ipotizziamo ora, con un test di pari sensibilità (99%) e specificità (99%), che la nostra malattia sia molto più diffusa: per esempio, supponiamo che la abbia una persona ogni 100. A questo punto testando un milione di persone il test identifica correttamente come positive 9.990 persone (in realtà sono 10.000) e come negative 980.100 (in realtà sono 990.000). Pertanto, tra le 19.800 persone che risultano positive al test, 9.900 sono realmente positive ma 9.900 sono in realtà negative. Se siamo positivi al test, quindi, la probabilità di essere realmente positivi è del 50%. Il test è lo stesso, ma rispetto alla malattia del primo esempio è cambiata l’incidenza nella popolazione. 

Torniamo ora al coronavirus. La settimana scorsa in Italia 680 mila persone sono risultate positive, quindi l’1,2% della popolazione italiana è risultato positivo. Ipotizziamo ora, considerando il continuo aumento del tasso di positività, che il numero di casi non trovati sia almeno pari a quello di quelli rilevati e che quindi la reale prevalenza sia intorno al 2,5%. 

Se a questo punto noi prendessimo casualmente un milione di persone in Italia e le testiamo tutte con un test con sensibilità e specificità del 99%, avremmo 24.750 veri positivi e 9.750 falsi positivi: con questi dati, la probabilità di essere realmente positivi, se si fa un test che risulta positivo, è quindi del 71,7%. I veri negativi sarebbero invece 965.250 e i falsi negativi 250, per cui la probabilità di essere in realtà positivi, se si fa un test che risulta negativo, sarebbe vicina allo 0%. Ma se applicassimo la prevalenza dell’1,2% la probabilità di essere positivi realmente dopo un test positivo scenderebbe al 55%.

Nella pratica, poi, non si testerà mai un milione di persone a caso. In Italia non abbiamo dati sul motivo per cui vengono condotti i test, ma è ragionevole assumere che una parte importante, in particolar modo in un momento con una così alta diffusione del coronavirus, riguardi chi ha sintomi o chi è stato a contatto con un positivo. Questo fa sì che la probabilità a priori non sia più dell’1,2% o del 2,5%, ma sensibilmente più alta: se ipotizziamo ad esempio che sia del 10%, in questo caso la probabilità di essere davvero positivi in un test che dà un risultato positivo è salita al 92%.

In conclusione, i test antigenici sono un ottimo modo per sapere rapidamente se si è positivi o meno, ma bisogna saper interpretare il risultato tenendo a mente che un test accurato al 99% non implica che il risultato sia corretto nel 99% dei casi.